中考数学线段最小值怎么算(绝密解题技巧，求最小线段和！)

解题技巧：求两个线段和的最小值

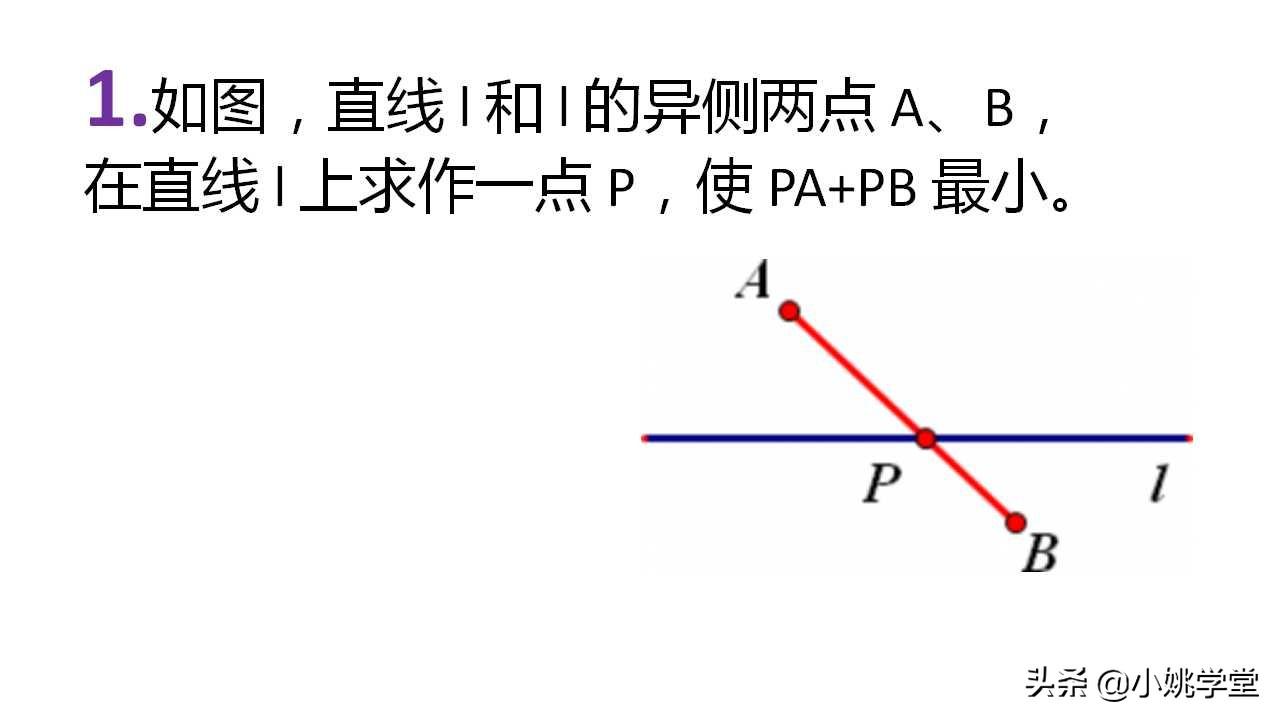
为了求两个线段和的最小值，我们可以利用两点间线段最短的概念。假设有点P和点Q，并且有一条直线上有一个动点O。我们需要求出什么时候PO加上Q的长度最短。我们知道，当动点O恰好移动到PQ与直线的交点上时，PO加上Q的长度最短，因为两点之间的线段最短。因此，当我们求两个线段和的最小值时，我们需要将这两个线段构造成折线的形式，并且它们要有一个公共顶点才能利用两点间线段最短来求出它们的最小值。

题目分析：CD加上BE的最小值

题目给出角ABC等于60度，BC等于8，AC等于10，并且AD等于CE。我们需要求CD加上BE的最小值。根据题目告诉我们两个线段相等的条件，我们可以推测出要构造两个全等三角形AD等于CE。为了满足这个条件，我们可以做一条辅助线CK平行于AB，并且让CK等于AC。然后我们再连接KE。由于辅助线CK平行于AB，所以角A等于角AK。根据题目中AD等于CE的条件，我们可以得到三角形CK全等于三角形CAD。因此，CD应该等于KE。然而，题目要求的是CD加上BE的最小值，我们可以将其转化为KE加上BE的最小值。由于KE和BE有一个公共点，形成一个折线的形式，我们可以利用两点间线段最短来求解。因此，我们需要连接KB，当点E移动到该点时，KE加上BE的长度最短。

辅助线的构造

我们可以假设CK平行于AB，并且点K位于该线上。然后我们让CK等于AC，并连接KE。由于CK平行于AB，角A等于角AK。根据题目中AD等于CE的条件，我们可以通过边角边得到三角形CK全等于三角形CAD。由此可得对应边相等，即CD等于KE。然后，题目要求的是CD加上BE的最小值，我们可以将其转化为KE加上BE的最小值。

求解最小值

为了求解最小值，我们需要计算KB的长度。我们可以做一个直角三角形，延长CK并在点B上画垂线，假设垂足为H。因为角ABC等于60度，所以角BCH为30度。根据三角函数中正弦函数的定义，CH等于4。在直角三角形BCH中，我们可以利用正弦定理求得BH的长度为4倍根号三。由全等三角形可知，CK的长度等于AC，即10。因此，KH等于14。根据勾股定理，在直角三角形KHB中，我们可以求得KB的长度为2倍根号下61。因此，KB的长度即为CD加上BE的最小值。

总结起来，CD加上BE的最小值为2倍根号下61。