初中数学的正切值是什么(惊呆！揭秘选梯子绝招，最陡梯秒变小黄的智慧选择！)

如何选择更陡的梯子：理解三角形比较

引言： 在小黄想要够到十米高台上的樱桃时，他面临了选择梯子的难题。在今天的数学微课中，我们将一起为小黄选择最合适的梯子，通过理解直角三角形和正切值的概念，帮助小黄选取最容易上去的梯子。

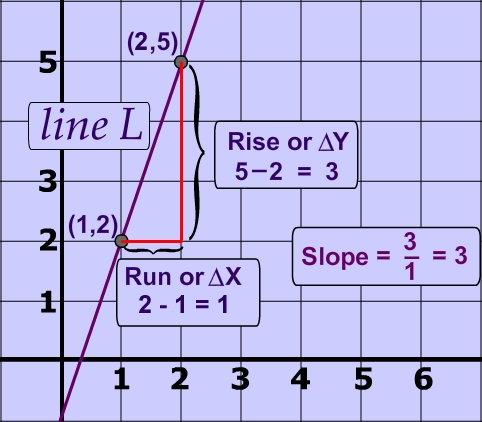
1. 梯子的陡峭程度与三角形关系： 首先，我们可以将梯子、墙和地面形成的形状看作一个直角三角形。其中，墙与地面为直角边，梯子为斜边。我们可以定义梯子的铅直高度为从梯子顶端到墙角的距离，梯子的水平宽度为从梯子底端到墙角的距离，而梯子与地面的夹角则称为倾斜角。

2. 三角形比较： 我们可以通过比较两个直角三角形来理解梯子的陡峭程度。当梯子的铅直高度相同的情况下，水平宽度越小，梯子就越陡。同样地，当水平宽度相同的情况下，铅直高度越大，梯子也越陡。实际上，我们可以将这个比较关系表示为梯子铅直高度与水平宽度的比值，即正切值。正切值越大，梯子越陡。

3. 正切值的概念： 在直角三角形中，角度A的正切值被定义为角A的对边与邻边的比值。换句话说，正切值表示铅直高度与水平宽度之间的比例关系。在RT三角形ABC中，当锐角A的大小确定后，角A的正切值也随之确定。

4. 特殊角度的正切值： 下面列出了一些特殊角度的正切值，这些值可以在数学计算中帮助我们更好地理解角度的陡峭程度。

• $\tan(0^\circ) = 0$
• $\tan(30^\circ) = \frac{1}{\sqrt{3}}$
• $\tan(45^\circ) = 1$
• $\tan(60^\circ) = \sqrt{3}$
• $\tan(90^\circ)$ 不存在（无穷大）

5. 选择更陡的梯子： 根据正切值的概念，我们可以得出结论：梯子的角度越小，坡度越小，越陡峭。因此，为了让小黄更容易够到樱桃，我们应该选择正切值较小的梯子。

6. 解题实例： 让我们通过两道题目来巩固所学：

题目一： 在RT三角形ABC中，角C等于90度，角A等于3，角B等于4，则角A的正切值为多少？

答案： 选择A。在这道题中，角A的正切值由角A的对边与邻边的比值决定，即$\tan(A) = \frac{\text{对边}}{\text{邻边}} = \frac{3}{4}$。

题目二： 如果角A是等腰直角三角形的锐角，角A的正切值是什么？

答案： 选择C。由于等腰直角三角形中，锐角A的两条直角边长度相等，所以$\tan(A) = \frac{\text{对边}}{\text{邻边}} = \frac{1}{1} = 1$。

结尾： 通过本节课的学习，我们已经了解了如何通过比较正切值来选择更陡峭的梯子。这个概念不仅在小黄够到樱桃的情境中有用，还可以在其他数学问题中得到应用。希望通过练习正切值的计算，你能更深入地理解数学的魅力，并在未来的学习中更加热爱这门学科。