初中数学怎么加辅助线(绝密技巧揭秘！快速解决几何辅助线难题！)

题目：如何巧妙地添加几何辅助线解题

引言：几何辅助线的添加技巧

在解决几何题目时，许多同学常常感到头疼，尤其是在找到适当的几何辅助线方面。本文将通过一个示例问题来介绍如何快速而巧妙地添加几何辅助线，并进行证明。

问题描述

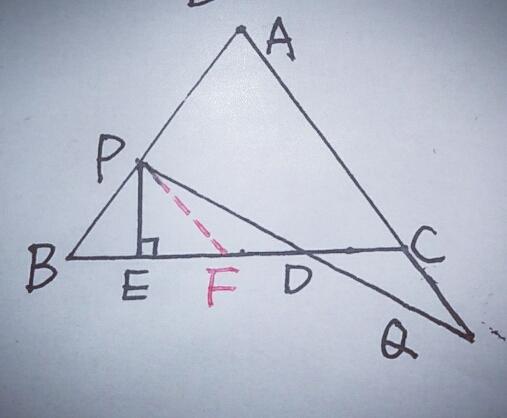
考虑三角形ABC，其中角B等于角C的两倍。我们设角C为α，那么角B是否等于2α？此外，我们知道线段AD垂直于线段BC，其中点M是BC的中点。已知AB的长度为10厘米，我们需要求出线段MD的长度。

猜想与观察

首先，我们应该猜测线段DM的长度可能与AB的长度存在某种关系。直观上看，DM与AB之间是否具有一半的关系？因此，我们初步猜测DM等于5。

现在，我们需要证明DM等于1/2的AB。在初中阶段，我们学到了一些与1/2或2倍相关的知识点，其中一个是中位线。中位线平行于底边且等于底边的一半。在这里，M已经是BC的中点，因此我们可以选择AC的中点N，并连接MN。根据直观猜测，MN是否等于AB的一半，即5？因此，我们需要证明DM等于MN。

证明思路

为了证明DMN是一个等腰三角形，我们需要连接DN并证明它是等腰三角形。注意到ADC是一个直角三角形，而N是斜边AC上的中点，因此DN是斜边的中线，应该等于斜边的一半。因此，三段线段都相等，使我们的角α位于这里。这个角度就是我们的α了，然后我们的中位线不仅等于底边的一半，还平行于底边，这导致我们的2α角也在这里，所以这个角就是我们的2α，这个角2α等于α，原因是一个外角等于它不相邻的两个内角之和。

结论

通过以上论证，我们已经得出DM等于MN，进而等于1/2的AB，因此答案为5。

其他方法

除了使用中位线，初中阶段我们还学到了斜边中线等于斜边的一半。如果我们想构造AB的一半，我们可以选择AB的中点P，并连接PD。这个PD就是斜边中线，也等于5。然后我们可以转换问题，需要证明PD等于DM。为了证明这一点，连接PM，然后证明PDM是一个等腰三角形。

总结

通过这个示例问题，我们展示了如何巧妙地添加几何辅助线并使用基本的几何知识解决问题。这些技巧包括中位线和斜边中线的性质，以及角的性质。希望这些方法能帮助同学们更轻松地解决几何问题。同学们可以尝试自己完善这些证明过程，并在评论区分享答案。