数学题初中如何构造圆(圆中的定长定角构造，求最小值)
别思芸
精选回答
鬼鬼讲数学
2023-08-06 09:24:56
定长定角构造辅助圆问题
问题描述
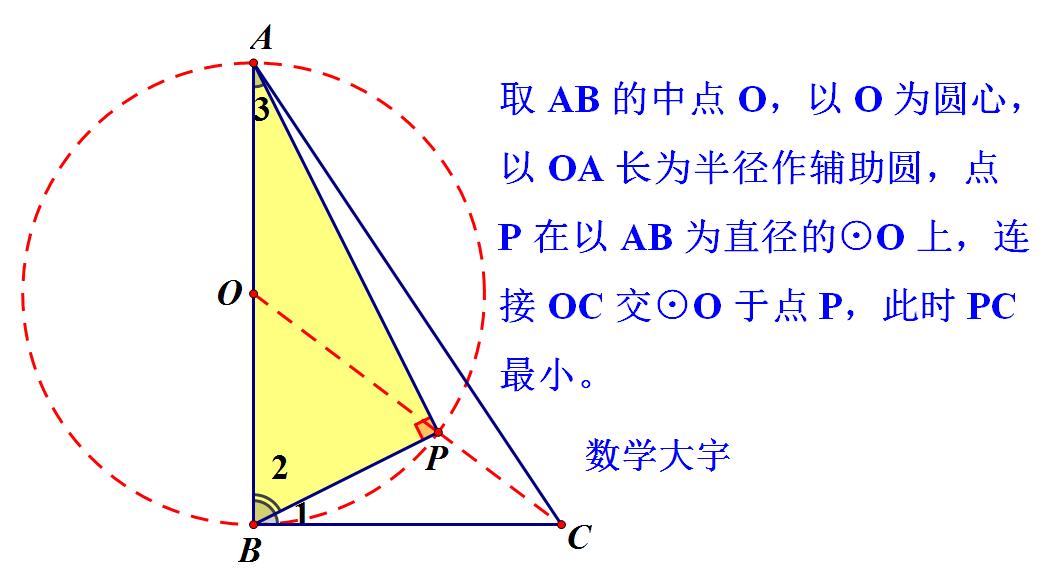
在矩形ABC中，AB等于2√2，AD等于4。P是矩形内的一个动点，且始终保持着∠APB=90度。求DDP的最小值。
解题思路
要求解DP的最小值，需要探究P的运动轨迹，而P的运动轨迹是一个关键点。根据题意，我们可以发现矩形ABC中的AB是一个直径，所以可以以AB的中点为圆心构造一个辅助圆。P点在这个圆上运动。
最小值分析
要求解DP的最小值，在圆中是圆外一点和圆上一点的最小值，即过圆心和圆上一点的线段最短。我们可以通过分析不共线情况下的三角形来解释这点。若不共线，则组成一个三角形，在这个三角形中，任意两边之和大于第三边，所以DP永远大于OD。而当OPD三点共线时，DP和OP的和等于OD，即DP最短。所以最小值出现在当OPD三点共线的情况下，此时OP的最小值等于OD减去OP。
计算最小值
OD在三角形AOD中是斜边，所以OD等于√(OA²+AD²)，即√(2²+4²)=√18。半径OP等于√2。所以最小值为√18-√2=2√2。
小结
通过本题，我们可以得出以下两个需要注意的问题： 1. 定长定角线圆形的问题：要找到直径所对应的圆周角为90度，构造一个辅助圆。 2. 最小值问题：通过穿心线的概念，即过圆心和圆上一点的线段最短，可以求得DP的最小值。
通过以上分析和计算，可以得出最终答案为2√2。
鬼鬼讲数学
2023-08-06 09:24:56
相关推荐
数学题初中如何构造圆(直角三角形斜边等于二，求最大值)
喻雯馨
直角三角形问题：求AC加两倍AB的最大值问题描述给定一个直角三角形，斜边BC的长度为2，求AC加两倍AB的最大值。解决方法为了解决这个问题，我们可以采用画折为直的方法。首先，将两倍的AB转化为与AC在同一直线上。我们可以在AC上延长一段长度为两倍AB的线段AD。接下来，将问题转化为求AC加AD的最大值，即求线段CD的最大值。为了求解CD的最大值，我们可以连接BD。根据题目条件可知，tan&alph
展开详情
初中几何数学题如何分析(超难几何题解密：构造辅助线轻松求最小值)
溥广阳
标题：线段加法最值问题的构造方法随着几何学难度的不断升级，解决线段加法最值问题已经成为一项具有挑战性的任务，尤其当涉及到需要构造辅助线将两个不相邻的线段合并时，问题变得更加复杂。在这篇文章中，我们将详细探讨如何构造这样的问题。1.已知条件首先，我们已知线段AB和线段AC相等，并且它们形成一个垂直等腰直角三角形，其中角度为45度。我们的目标是找到线段ae加上CD的最小值。通常，解决这类问题的方法可以
展开详情
初中数学圆是什么题型(初中数学：探究圆相关题型)
都之桦
初中数学中，关于圆的题型涉及多个方面，包括但不限于以下几种常见题型：圆的基本性质：涉及圆的基本概念，例如圆的直径、半径、圆心、圆周、弧长等，以及它们之间的关系。这类题型通常考察学生对圆的定义和性质的理解。圆的面积和周长计算：要求计算圆的面积和周长，涉及公式的运用，如圆的面积公式（πr²）和周长公式（2πr）。学生需要根据给定的半径或直径计算圆的面积和周长。相交圆的性质：考察相
展开详情
初中数学圆如何表示直径(圆的直径计算公式是什么？学习初中数学一起学习)
习华素
同学们好，我是罗老师，今天我们来看一下这道题，圆的直径计算公式是什么？圆的直径计算公式是D的圆派分之C。接下来我们详解下这道题，如果这里有一个圆，那么这个有个圆心O，然后它的半径是这一截R，那么我们再延长这个AB就是它的直径，那这里的也就等于D也就是2R，而圆的周长公式C等于二派R，所以我们要用直径来表示就为拍D，因此我们通过周长来求它的直径就为D等于派分之C。当然除了周长来求直径，我们也可以通过
展开详情
初中数学题怎么做的好(初中数学题高效破解)
燕雄荣
初中数学题解题技巧数学在初中阶段是关键科目之一。以下是解题技巧：1.仔细审题认真阅读题目，明确问题要求，理解题意是解题的关键。2.掌握基础知识深入理解基础知识点，如四则运算、代数等，是解题的基础。3.多维思考尝试从不同角度解决问题，采用多种方法求解，培养灵活的解题思维。4.勤于练习多做题目，包括课堂练习和额外练习，巩固知识点，熟悉题型。5.识别考点认清题目中的考点，解题时着重处理核心内容，快速捕捉
展开详情
初中数学实心圆和有什么()
幸初彩
题目：探究规律，计算空心圆的数量引言：在这道题中，我们将研究一种图形排列的规律，其中实心圆和空心圆以不同方式表示。通过观察一段排列的规律，我们将尝试解决一个问题：在前2020个圆中，有多少个是空心圆？发现规律：首先，我们观察到排列如下：一个11个空心，两个11个空心，三个11个空心。然后，后面是一个实，一个空心，两个实心，一个空心，三个一个空。规律分析：-我们注意到这个排列是不断重复的，每个片段都
展开详情
初中数学题怎么变通(惊人算术技巧：解决最难数学题！)
杭嘉梦
题目：解析数学难题难题解析：题目描述：给定条件：X大于零，求表达式根号下X的平方加四，再加上根号下12减X的平方加九的最小值。解题思路：勾股定理应用：当遇到根号下一个数的平方加另一个数的平方时，可以利用勾股定理的概念。在这里，我们可以将它看作一个直角三角形，其中两条直角边分别是2和X，斜边长度为根号下X的平方加上2的平方。分析第二部分：同理，另一个式子也可以被看作一个直角三角形，其中直角边分别是1
展开详情
初中数学题怎么学才会简单(用最简单的思路解决最难的题)
廖桦林
这是一道初中几何的经典好题，来看一下三角形ABC中，Ad垂直BC于D，那这里的ad就是一条高，并且已知bad等于二，CD等于三，还告诉我们这个三角形的一个内角BAC等于45度，最后要我们求这条高线的长度。如果你之前见过这道题，你大概率见到的可能是做轴对称构造这个正方形，也就是半角模型，或者是构造辅助圆，或者是用高中的超纲的三角函数知识。但是在我看来，这些方法都是舍近求远，其实我们按照最基本的思路就
展开详情
如何识别初中数学题(初中数学必备：如何区分整式与分式)
叶赫那斌彦
大家好，我是小鹿老师。今天我想和大家分享一道初中阶段的数学选择题，即如何区分分式和整式。首先让我们先了解一下这两个概念。整式是由单项式或多项式组成的，例如：5A、5或者A+5，其中单项式就是只含有一个变量的项，多项式则由多个单项式组成。而分式可以理解为分数的形式，其中分母必须是一个阿拉伯数字，不能包含未知数。如果一个式子的分母包含未知数，则它是分式，否则它是整式。举个例子，如果我们有一个分子为3A
展开详情
初中数学有哪些有趣的(初中数学乐趣探索)
应娅阳
探寻初中数学的有趣之处初中数学是一门充满乐趣和挑战的学科，其中有许多有趣的内容值得探索：几何与图形初中数学的几何部分涉及图形的性质、构造和计算，如三角形、圆、多边形等，充满了趣味和美感。数学游戏与解谜数学可以通过游戏和解谜来加深理解，例如数学逻辑游戏、数独等，激发学生的思维和动手能力。数学实际应用数学的实际应用领域包括概率统计、数据分析等，通过真实场景的应用，让数学变得生动有趣。数学的奇妙定理介绍
展开详情
初中数学的正切值是什么(绝密口诀！轻松秒杀求解tan15度的神奇方法！)
江灵枫
标题：构造法求解tan15度的方法与原理引言：初中数学中，三角函数是一个重要的概念，而求解特定角度的三角函数值有时可能会变得相对复杂。然而，通过巧妙的构造方法，我们可以轻松地求解tan15度的值，而不需要繁琐的计算过程。本文将介绍一个简洁而实用的方法，帮助学生们理解如何求解tan15度，并逐步解释构造的原理。1.构造30度的直角三角形：首先，我们知道tan30度等于根号3的三分之一。为了构造这个问
展开详情
数学有什么思想初中(绝妙化归技巧，解决数学难题！)
葛馥美
初中数学中的重要思想：转化与化归引言初中数学中，转化与化归是关键思想。当面对陌生问题时，我们通常需要通过构造方法将问题转化为更熟悉的形式。本文将通过一个示例来说明这一思想的应用。问题的背景我们经常遇到这样的问题：需要构造一个整式的值，通常是通过构造同底数或同指数的方式。然而，某些问题可能要求我们计算一个分式的值，这与通常的整式不同。当我们遇到这种陌生问题时，该如何应对呢？问题解决的关键：构造与化归
展开详情
