初中地理等高线题怎么做(等高线的秘密，你可能不知道的真相！)

等高线的问题

引言

在等高线问题中，许多孩子认为这些题目比较难，但实际上大部分等高线题还是比较容易的。当然也不排除在等高线中有一些具有难度的问题。

求山顶的高度

我们来看一个例题，求解这个图中山顶的海拔高度。观察这个图，我们发现在某个位置有一个山顶。那么这个山顶的海拔高度是多少米呢？

问题分析

我们注意到这张等高线图的边缘是被切割的。接下来我们需要补充这个等高线，特别是观察到海拔为200米的等高线在某处突出。我们可以将这条突出的线进行补充，得到一个高度为200米的线段。

高度推导

通过推导，我们可以得出这条线的高度依次为300米、400米、500米。因此，这个山顶的高度应该在500米到600米之间。

注意边缘部分

我们发现这个问题的关键在于对等高线边缘部分的补充。因为等高线在图中的截断部分是不完整的。所以我们需要将其理解清楚，并对边缘部分进行适当的补充。

类似问题

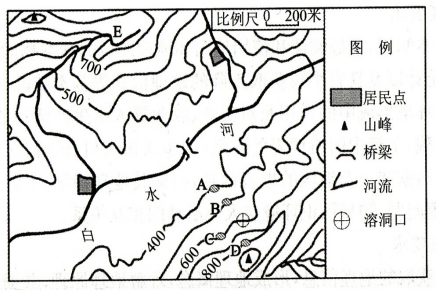
类似这样的问题也有其他的例子，比如我们山东潍坊就考了这样一个题目。同样地，它的等高线边缘也是被切割的。问题是求图中最大的相对高度是多少米？我们找到最高的地方并观察其高度，它位于600米到700米之间。同时，我们还可以找到最低点，将其标注出来。

清晰边界

我们注意到问题中存在一个阴影区域，即最低点。在考虑这个问题时，我们需要注意的是红色斜线的高度应该在0米到100米之间。因为我们观察到图中有一条河流，而水是向低地流动的。如果红色斜线也是200米，那么A点就会比较低，而B点则较高，这与实际情况不符。

画出正确的线段

因此，我们推导出红色斜线的正确高度应该是从200米向下弯曲，即低于200米。同时，我们也发现等高距为100米。因此，对于蓝色线段而言，高度应为0米到100米。

总结

在等高线问题中，我们需要仔细观察和思考。有时候会遇到类似的问题，比如直接判断山脉的走向等。因此，对于等高线的应用，我们需要深入理解并进行分析。