冰淇淋模型与特殊三角形构造求解难题

引言

在解决数学难题时，我们常常需要借助一些模型来简化问题的复杂度。本文将介绍利用冰淇淋模型和特殊三角形构造方法解决一个复杂三角形问题的思路和步骤。

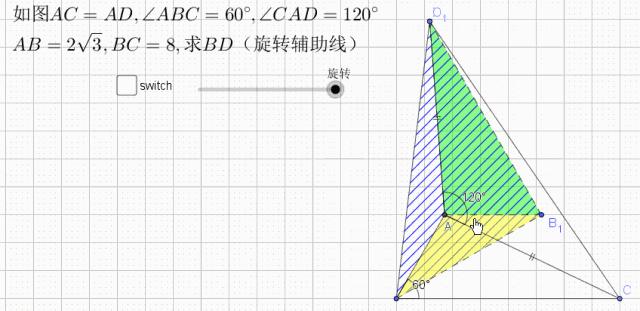
问题描述

给定一个三角形ABC，以边AB为基础，向外构造一个等腰直角三角形，连接PC，并求线段PC的长度。

冰淇淋模型与特殊三角形构造

在初中阶段，我们常见的特殊三角形有两类，一类是等边三角形，一类是等腰直角三角形。利用冰淇淋模型，我们可以将一个特殊三角形与一个普通三角形结合，形成一个更复杂但更易于处理的图形。

具体针对该问题的构造方法如下： 1. 以三角形ABC中的边AB为基础，向外构造一个特殊的等腰直角三角形，构成了一个类似冰淇淋形状的图形。 2. 注意到构造的等腰直角三角形的直角顶点与原有等腰直角三角形的直角顶点重合，因此我们以A为直角顶点，构造另外一个边为AP的等腰直角三角形。

构造相关三角形与求解

在构造过程中，注意到新构造的三角形与原有的等腰直角三角形具有相同的形状。因此，我们只需在剩余两条边中任选一条，构造与已有等腰直角三角形相似的形状即可。

接下来，我们以构造三角形DB为例进行说明。根据全等三角形的性质，我们可以知道三角形APC与三角形DBC全等，即它们的对应边相等。

由于题目要求求解PC的长度，我们可以将PC连接起来，同时设中间角为α。观察到三角形ACD和三角形APC具有相同的绿边和黄边，并且它们的夹角都等于90°+α。

进一步观察，我们可以发现三角形DBC与三角形ACD也有相同的绿边和黄边，并且它们的夹角也等于90°+α。因此，我们可以将DB连接，构造全等三角形。

现在，我们需要求解线段BD的长度。根据特殊直角三角形的性质，我们知道45°角的等腰直角三角形的一条直角边长度为4倍根号。根据勾股定理或特殊直角三角形的三边比例关系，我们可以求得斜边长度为8。

接下来，我们进一步简化问题。将45°角与75°角相加得到120°，将BD放在一个这样的三角形中，一边为2，一边为8，夹角为120°。因为120°的邻补角为60°，我们可以得知过点D做垂线会形成一个直角三角形。

观察到该直角三角形中的角度关系，我们可以知道该角为30°，而对应的直角边长度为斜边的一半，即为4。

在此直角三角形中，同样可应用勾股定理或特殊直角三角形的三边比例关系，我们可以求得该直角边长度为4倍根号3。

综上所述，整个大的直角三角形中，一边为4倍根号3，一边为4+2=6。利用勾股定理，我们可以求得BD的长度为2倍根号2。

结论

通过构造特殊三角形和应用相似、全等三角形等几何性质，我们成功求解出了线段PC的长度为2倍根号2。该方法有效地简化了原问题的求解过程，并通过冰淇淋模型将复杂问题转化为相对简单的几何图形推理。